# Interaction ---- # An interactive multimodal app: PONG Let's create a game. Let's rebuild one of the oldest and most famous computer games of all time: **PONG!**  > Pong is one of the earliest arcade video games; it is a an electronic ping-pong game featuring simple two-dimensional graphics. Pong was one of the first video games to reach mainstream popularity. The game was originally manufactured by Atari Incorporated (Atari), who released it in 1972. Pong quickly became a success and is the first commercially successful video game, which led to the start of the video game industry. Pong has been referenced and parodied in multiple television shows and video games, and has been a part of several video game and cultural exhibitions. [wikipedia](http://en.wikipedia.org/wiki/Pong) ## The Game > The player controls an in-game paddle by moving it vertically across the left side of the screen, and can compete against either a computer controlled opponent or another player controlling a second paddle on the opposing side. Players use the paddles to hit a ball back and forth. The aim is for a player to earn more points than the opponent; points are earned when one fails to return the ball to the other. [wikipedia](http://en.wikipedia.org/wiki/Pong) [Here is an early video from 1969.](http://www.youtube.com/watch?v=XNRx5hc4gYc) [Here is an early Atari version](http://www.youtube.com/watch?v=SHsYjWm8XSI) [Another Atari version from 1972 with different sounds](http://www.youtube.com/watch?v=3nu_L8uEzJw) To rebuild Pong we should analyze the important components and subcomponents, to make sure we can implement each one, until the entire game is complete. **Divide and conquer** is the foremost idiom of software design. At the most general level most games incorporate these components: - **Game state**. (Sometimes called the **model**). The data that describes the state of the game at any moment, including the world and its objects, meta-level data such as scores and modes, resources used in rendering, and so on. - **Game logic/simulation**. (Sometimes called the **controller**). The **update** routine(s) that modify the game state from one step to the next. It may be composed of several subroutines for different (kinds of) objects, and may have routines that operate in parallel. - This includes **interaction**. The ways in which a player can add new input to the game logic as it is simulated, such as keyboard, mouse, joystick, head-tracking and other human interface devices (HIDs). - **Rendering**. (Sometimes called the **view**). How the game is visualized and sonified. ## Game State The game comprises these elements: - Two players, represented by the "paddles" on screen. - Each player has a paddle that can move up and down the screen (and also left to right in the original demo) - That means we will also need variables to store the vertical velocity. - Each player also has a score. - One ball, with variable X and Y position. - The ball moves continuously until a collision occurs. - That means we will also need variables to store the ball horizontal and vertical velocity. - (*The original design also had support for spin, or "English"*) - Configuration parameters to tune the gameplay. ## Game logic Most of the game dynamics come from the movement of the ball. These are the basic properties of Pong. - The game is played in rounds. A round starts by serving the ball, and ends by scoring a goal. - At the start of a round, the ball begins in the center of the screen with a random direction of motion. - The ball moves by continual accumulation of velocity to position. - Exceptions to this rule depend on collision detection: - If the ball touches the top or bottom edge of the screen: - It bounces (reversing the vertical direction) - If the ball reaches the left edge of the screen: - Player 2 gains one point - A new round is started - If the ball reaches the right edge of the screen: - Player 1 gains one point - A new round is started - If the ball collides with the inside face of a paddle: - It reverses horizontal direction - *It speeds up slightly, to make the game get harder.* - *It changes vertical direction slightly, depending on which edge (top or bottom) of the paddle it collided with.* The trickiest part of that is detecting whether the paddle has hit the ball. We can break that down into two conditions: - The Y position is between the top and bottom edges of the paddle. - The old X position was in front of the inside face of the paddle, and the new X position is on or behind the inside face of the paddle. *In fact this is not quite accurate, but good enough to start with.* ## Interaction - **Paddles**: players can move the paddles up and down the screen. - For a two-player game, we'll need to use keypresses to move the paddles. - We can detect when a key is pressed, and modify a paddle velocity according to what key it is. - We can detect key release set the paddle velocity back to zero. - Or we could use mouse interaction - We also need to invent one or more algorithms for the computer's playing style... - It should play better than random, but worse than perfect! - Paddles should also be restricted from reaching the top or bottom of the screen. - *In the real Pong game, they couldn't even quite reach the edge, so there was always a chance to score against a pro.* - Options: we might want to use other keypresses to choose options: - A key to reset the game & scores to zero - A key to pause the game - Whether to play 2-player mode or 1-player versus computer? Or detect that automatically by lack of keypresses? ## Rendering Pong The rendering of the original Pong is incredibly simple, made entirely of large black or white squares, to represent the essential elements of paddles (players) and the ball. The sounds of Pong (if present at all) were similarly simple, reflecting the available technology of the day. Wwe might want to try rendering in a more elaborate style. Our game sounds could include a combination of: - A background music track - Triggered sound events: - When a round begins - When the ball collides with walls - When the ball collides with a player paddle - When a goal is scored ## Assignment: Elaborating Pong We quickly sketched up a working version of Pong in class: https://github.com/grrrwaaa/gct633/blob/master/classfiles/oct29.lua (If you pull the latest copy of the class software, you will have this file already). The task of this assignment is to elaborate, mutate or otherwise rewrite Pong in two or more interesting ways. We began to explore some possible directions in class, but whether you follow them or implement your own ideas, try to take them as far as possible in the time available; and enjoy exploring! Perhaps it will evolve into an entirely new game; perhaps it won't even be a game anymore... We can discuss your ideas during class, in office hours, or by email. ### Grading This is a bigger assignment than the previous ones, and contributes 3x more to your grade; please dedicate more time to it accordingly. And have fun doing it! Grading will take into account the creativity/novelty of your ideas, the technical execution of them, and the aesthetic/perceptual quality of the result. You may be asked to present your game to the class. ### Submission details If your project uses more than one file, please remember to upload them all. If you use sound files, make sure that they are not more than a few seconds long, and upload them too. You must comment your code thoroughly. At the top of your main script please include a long comment that includes: - A description of your project idea(s) - An explanation of how to use it (what the interaction is, how the gameplay works) - Your strategy to implement your ideas, and any challenges you had implementing them - Your ideas for how it could be taken further in future work (*important!*) In addition, there should also be a comments throughout the code: - For each function, to explain what it does - Comments over any complex or important lines in the code - Comments to note where there might be possible errors - Comments to indicate where possible future work could be added ("TODO" comments) Remember: good code formatting and commenting is part of the technical execution. Code is for humans as well as machines! ### Example ideas: - Sound: - Using more interesting sounds! - Using more game feature parameters to modify the sound synthesis, e.g. the angle of bounce, speed, etc. - Adding a backing track (like the drum machine) that dynamically adapts to the gameplay - e.g. setting the tempo according to the ball speed - Adding sound effects on the sounds: echoes, distortions etc. - Ball: - Adding nonlinear movements, like "spin" ("English") - Pong with multiple balls! - Adding a gravitational field with black holes to influence the ball - Paddles: - Adding paddle rotation - Changing paddle size (or shape) according to the current score - Sticky paddles - Multiple paddles in flocking formations - Paddles that reproduce and die - World: - More obstacles in the space - Adding portals (quantum-tunneling pong!) - Time: - Making the ball move in rhthmic bouncing jumps instead of a smooth line - Extra paddles that follow your movement with delay - Extra points for scoring a goal 'on the beat' of the rhythm - Pong with different rules and systems on each 'level' (each subsequent round of the game) - AI: - Different NPC player 'personalities' - An opponent that learns from you? - Visual: - More complex geometry in the VBO - Pong in 3D space... [For inspiration: taking pong way too far...](http://www.youtube.com/watch?v=NDjseVmruH8) ----- # Sound toys Sound toys are small applications with interactive visual interfaces that generate sound. Some are desktop apps, some are web apps, and in recent years there have been many mobile apps (often reconstructing earlier desktop or browser based works). Some are more like instruments, some are more like games, some are more like interactive media artworks, or audio-visual paintings, others are not easily categorized. They are a useful medium for us to explore, as they are often quite interesting in behavior despite the simplicity of design. Often they use drawing input, simple physical simulations, network or agent systems in the creation of interesting interfaces and behavior. - One of the oldest selections of web-based soundtoys is at [www.soundtoys.net](http://www.soundtoys.net/), though some of them don't work on modern browsers. - A more recent selection is at [creative applications net](http://www.creativeapplications.net/tag/soundtoy/) - A pioneering collection of sound toy experiments is the [ixi software collection](http://www.ixi-audio.net/content/software.html). They might not work on your OS, but there is source code. You might find videos of them on Youtube. - An academic treatment by one of the authors: [ixi software: The Interface as Instrument](http://www.ixi-software.net/thor/ixi_software.pdf). - Golan Levin created a series of audiovisual experiments for his [MIT Masters thesis](http://www.flong.com/texts/publications/thesis/) such as [YellowTail](http://vimeo.com/661922). See also his [TED Talk on software as art](http://www.ted.com/talks/golan_levin_on_software_as_art.html) - Artist Scott Snibbe studio reconstructed several earlier works for iOS, such as [bubbleharp](http://www.snibbestudio.com/bubbleharp/) - Some simple but novel ideas have grown into complex applications, such as [Nodal](http://www.csse.monash.edu.au/~cema/nodal/). Despite the complexity, the core idea in Nodal is simple: nodes are instruments, laid in a grid with connections along which players constantly move. - [Academic paper](http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.146.2797) - The game [*fLOW*](http://www.xgenstudios.com/game.php?keyword=flow) began as a student project at UCLA, in which you guide a growing fish-like creature around a space eating smaller fish, and going up and down levels as desired (based on the psychological concept of "flow"). It was picked up by SONY for the [Playstation](http://us.playstation.com/games/flow-ps3.html). ## Assignment 4: Propose/analyze a sound toy Do some research looking at existing sound toy applications and related artworks, experiments, software instruments and so on. Either choose one that you like, or invent a new idea inspired by one or more existing sound toys. It should include graphics, sound and interactivity; and it should be fairly simple yet creative, interesting, novel and/or fun. > Even a simple system can become publishable research or a marketable product if it is interesting, fun and novel. What you need to do is: 0. Indicate the inspirational references (ideally a website / video). 1. Describe the project briefly (2-5 sentences), including the main components, the kind of interaction. Articulate why it is innovative, interesting or fun, despite the simplicity. 2. Outline the implementation challenges in more detail: break down the application into each of the components, including the sound and graphical rendering, the simulation, and the interaction. For each one outline areas that could be more challenging. 3. From this you can identify what is the global state the program would probably need. This is a proposal for your final project, so the deadline is very short. You can submit an individual idea for this assignment but join a team with somebody else's idea for the final project if you prefer. Working in teams may be necessary for more challenging projects. ## Example Let's take the example of [Soundrop](https://itunes.apple.com/en/app/soundrop/id364871590?mt=8), which has been fairly successful on the difficult iOS app market.  ### Summary: You can draw platform surfaces into a space, on which balls can bounce. Each bounce makes a sound depending on the ball's speed. Balls appear at one point in space, and are subject to gravity. By drawing, erasing, moving the lines you can create small musical systems. Despite the simplicity it is quite addictive, perhaps because it scales well: you can really puzzle through building up a complex system part by part, and it sounds engaging at all stages. ### Implementation: - Simulation: - A moving ball - Position and velocity - With force of gravity - Also need forces (acceleration) - Bouncing of surfaces at different angles - Challenge: collision test: intersection of ball-path with surface - Collision effect: calculate change in forces and new ball position - Many surfaces, many balls - Balls generated periodically at one location - Balls removed if they fly off the screen sides or bottom - Rendering: - Graphics: - Balls - Surfaces (endpoints and connection) - Sound: triggered by ball-surface collisions make sound - The pitch appears to depend on the ball velocity - Interaction: - Adding a surface - Drawing gesture: mouse start and end positions - Removing a surface - Challenge: Selecting a surface (with double-click or keydown?) - Requires mouse/surface collision test - Moving surface endpoint - Challenge: Selecting endpoint and dragging - Requires mouse/endpoint collision test - Moving the ball generator - Challenge: Selecting generator and dragging - Requires mouse/generator collision test ### State: - variable list of balls - position, velocity - ballsource position - variable list of surfaces - two endpoint positions (possibly and/or center + rotation?) - currently selected surface / endpoint - configuration - force of gravity ### Challenges: 2D line intersection & bounce reflection We want to know if the path of a ball over one time step will cross a particular "surface" line. If there is an intersection then we want to know where, and at what angle, so that we can accurately represent the bounce. We also need to be careful for special cases: if the two lines share an endpoint, or if the two lines are parallel. The line intersection discussion is borrowed from the pages at [Paul Bourke's excellent website](http://paulbourke.net/geometry/pointlineplane/).  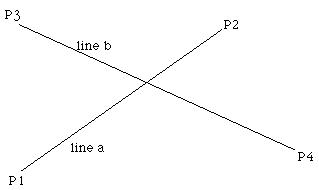If we are given a line segment as two points P1, P2, then we can also represent it in terms of an origin plus a slope and scalar: "P1 + uD"; where the slope "D" is derived as "P2 - P1". > For the ball, P1 is the current position and D is the velocity. This should also look familiar from linear interpolation we have seen before; the only difference is that now P1 and P2 are of type vec2: ``` -- return the linear interpolation of p1 and p2 by factor t: function lerp(P1, P2, u) return P1 + u * (P2-P1) end ``` For two lines, we have: - Pa = P1 + ua( P2 - P1 ) - Pb = P3 + ub( P4 - P3 ) To derive the point where these lines meet, we must solve for Pa == Pb. 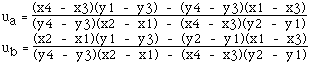Separating the X and Y components: - x1 + ua (x2 - x1) = x3 + ub (x4 - x3) - y1 + ua (y2 - y1) = y3 + ub (y4 - y3)  > Paul Bourke notes that if the denominators are the same for both equations. If it is zero, we have parallel lines which cannot intersect. [Here is his C code](http://paulbourke.net/geometry/pointlineplane/pdb.c) For more optimzation, we'd like to abort the test as early as possible. One way is to make an **axis-aligned bounding box (AABB)** check: does any point on the path of the ball lie within the bounding box of the surface? If not, no intersection can occur. > A more optimal method is to use a sweep line method, as described [here](http://en.wikipedia.org/wiki/Line_segment_intersection). We might be able to simplify in our case knowing that the surface objects are "static": we can store them in a list that is sorted by horizontal or vertical position, and quickly narrow our search to an appropriate subsection of this list. In Soundrop the the ball velocities are more likely to be greater in the vertical direction (because of gravity), so a horizontal sort probably makes more sense. One we derive ua, we can determine if it lies between the segment boundaries: if ua >= 0 and ua <= 1, and ub >= and ub <= 1, we have a coordinate between P1 and P2, i.e. on the line segment. This will tell us how much bounce we need to add (1-ua). It also gives us the point of intersection itself: ``` -- point of intersection of the bounce: I = lerp(P1, P2, ua) -- amount of distance remaining to be applied in the bounce: speed = D1:length() remain = (1 - ua) * speed ``` For the bounce itself, we also need to calculate the reflection direction. [Paul Bourke also describes general reflection here](http://paulbourke.net/geometry/reflected/).  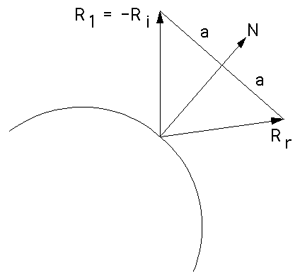First we convert D to a unit vector: ``` Ri = D1:normalizenew() ``` We also need a unit normal vector for the surface, which in 2D we can simply generate by an axis rotation followed by normalization: ``` N = vec2(D2.y, -D1.x):normalize() ``` > Note that this only needs to be calculated when the surface is created or modified; it thus makes sense to store the normal vector in the surface object itself. Then the reflection equation gives us a unit vector in the reflected direction: ``` Rr = Ri - 2 * N * Ri:dot(N) ``` So the final calculations for the bounce are: ``` -- new position of ball: B = I + Rr * remain -- new velocity of ball: V = Rr * speed ``` ### Challenge: selecting endpoints, lines, and generators The mouse itself can be considered a point. The line endpoints and the generator can be considered a circle. So to detect if the mouse has been clicked on a particular object, we need to do a point-circle intersection test. This is simple: if the length of the line from the mouse to the center of the circle is less than the radius of the circle, the mouse is inside the circle. For the line segments, we have to do something more complex. Here it is almost impossible for the mouse to be exactly over the line. So our options are to either consider the mouse a circle and do line-circle intersection, or to find the nearest point to the line and test whether the distance is less than a certain threshold. Again, [Paul Bourke](http://paulbourke.net/geometry/pointlineplane/) gives a good explanation for calculating the minimum distance to a line. Once we know that a particular object is selected, we can redirect mouse drag events to update that object's position. If the object is a line endpoint, it should also cause the recalculation of the line's slope and normal. ---- # Movement, behavior, force and vectors Several proposed projects include physical simulations or behaviors and object interactions. So here's a quick walk-through of using vectors for forces and behaviors. I'll use the two-dimensional [vec2](http://grrrwaaa.github.io/gct633/docs/modules/vec2.html) for now; however most of these concepts can be easily extended to [vec3](http://grrrwaaa.github.io/gct633/docs/modules/vec3.html) for three-dimensional cases. A vector can be used to store any property that has a magnitude and direction. It represents this in terms of components of principal axes. Examples include: - absolute location (i.e. vector relative to the spatial origin) - relative location (e.g. the path from object A to object B, or a line segment for drawing shapes) - velocity - acceleration, force If an object has a location in space, we can move it by adding a relative motion vector to the location. If we add this motion repeatedly, e.g. on each game update, we create the illusion of continuous movement. In this case the motion is a *velocity*. The repeated addition is called *integration*. Put another way, the velocity is a discrete approximation of the location's *first derivative*: modeling how it changes over time. ``` local window = require "window" window:create() local vec2 = require "vec2" local draw2D = require "draw2D" location = vec2(-1, 0) velocity = vec2(0.01, 0.01) function draw() -- integrate velocity to location: location:add(velocity) print(location) draw2D.point(location.x, location.y) end ``` The *second derivative* of location is *acceleration*: ``` local window = require "window" window:create() local vec2 = require "vec2" local draw2D = require "draw2D" location = vec2(-1, 0) velocity = vec2(0, 0) acceleration = vec2(0.01, 0.01) function draw() -- integrate acceleration to velocity: velocity:add(acceleration) -- integrate velocity to location: location:add(velocity) draw2D.push() draw2D.translate(location.x, location.y) draw2D.circle(0.05) draw2D.pop() end ``` Acceleration is defined by Newton in terms of *force*: *F = ma*. "Force = mass * acceleration", therefore "acceleration = Force / mass". Let's wrap this into an object called "agent": ``` local agent = { location = vec2(0, 0), velocity = vec2(0, 0), acceleration = vec2(0, 0), force = vec2(0, -0.1), mass = 100, } agent.move = function(self) -- calculate acceleration: self.acceleration = self.force / self.mass -- integrate velocity: self.velocity:add(self.acceleration) -- integrate location: self.location:add(self.velocity) end agent.draw = function(self) draw2D.push() draw2D.translate(self.location.x, self.location.y) draw2D.circle(0.05 * self.mass * 0.01) draw2D.pop() end function draw() agent:move() agent:draw() end ``` In this case we have modeled an object that is continuously subject to a force of (0, -0.1). This would be something like the effect of gravity. Other continuous forces might be e.g. the effects of a force of wind. The wind itself may be changing direction over time: ``` function wind() return vec2.random(0.1) end -- (in agent.move) self.force:add(wind()) ``` Or may also vary over space: ``` function wind(location) return location * -0.1 end -- (in agent.move) self.force:add(wind(self.location)) ``` However most forces a body interacts with are approximately instantaneous, rather than continuous. For example, if mouse is clicked, we could add an instantaneous jump force: ``` function mouse(event, button, x, y) if event == "down" then print("jump") agent.force:add(vec2(0, 4)) end end ``` This should only take effect for one simulation frame, rather tha continuously. To model this we can modify our *agent.move()* method to reset the force to zero and re-apply any continuous forces: ``` local gravity = vec2(0, -0.1) agent.move = function(self) -- add continuous force(s): self.force:add(gravity) -- calculate acceleration: self.acceleration = self.force / self.mass -- force has been applied; reset it: self.force:set(0, 0) -- integrate velocity: self.velocity:add(self.acceleration) -- integrate location: self.location:add(self.velocity) end ``` ## Constraints Pretty soon the object leaves visible space. You might want to handle this in different ways: - Limit movement to the boundary: ``` -- prevent location component going below -1 if self.location.y < -1 then self.location.y = -1 end -- or more simply apply to all limits: self.location:min(1):max(-1) ``` - Limit movement to a distance (i.e. a circular space): ``` self.location:limit(1) ``` - Wrap movement at the boundary: ``` -- wrap at x boundaries: if self.location.x > 1 then self.location.x = self.location.x - 2 elseif self.location < -1 then self.location.x = self.location.x + 2 end -- or more succintly, for both x and y: -- to wrap in the range -1,1, first shift to the range 0,2, then modulo the boundary, then shift back to -1,1: self.location:add(1):mod(2):sub(1) ``` - Detect when the location exceeds boundaries and execute arbitrary code. For example, create a force to change direction if the boundary is reached: ``` -- the fraction of energy lost when a bounce occurs: local friction = 0.1 -- bounce at ground level: if self.location.y < -1 then -- first clip object location at the boundary: self.location.y = -1 -- then apply bounce force in the positive y direction -- magnitude is proportional to object velocity and mass -- direction is reflected around the surface (hence multiply y by -2) local bounce = self.velocity.y * self.mass * -2 -- add this force self.force:add(vec2(0, bounce)) end ``` Other forms of constraints can be limiting movement to a line, or path. In this case the force applied can either be rotated into the line of the path, or only the component of the force along the path applied (this can be achieved using the dot product: "force = force:dot(path:normalizenew())"). Another very common constraint is to limit the velocity to an absolute maximum: "velocity:limit(max)". ## Many agents The way we have designed *agent.move* and *agent.draw* allows them to be applied to many agents. We could create a list of agents, and initialize them differently: ``` local agents = {} for i = 1, 100 do agents[i] = { location = vec2.random(), velocity = vec2(), acceleration = vec2(), force = vec2(), mass = math.random(200), -- "inherit" the move and draw methods from agent: move = agent.move, draw = agent.draw, } end ``` Then all we need to do is update our *draw* routine to visit each one of them: ``` function draw() for i = 1, #agents do agents[i]:move() end for i = 1, #agents do agents[i]:draw() end end ``` However, special care needs to be taken if the agent.move() function includes behavior between different agents (gravitation, spring forces, flocking, etc.). In order to make sure the effect of A on B is equal to the effect of B on A, you must separate the force calculation from the velocity/location integration into multiple passes: ``` agent.update = function(self) -- calculate forces and acceleration here end agent.move = function(self) -- update velocity, and location here end function draw() for i = 1, #agents do agents[i]:update() end for i = 1, #agents do agents[i]:move() end for i = 1, #agents do agents[i]:draw() end end ``` ## More forces ### Friction A crude simulation of air friction operates in the opposite direction to movement, with a constant magnitude. We can get the magnitude of a vector (it's length) by Pythagoras's theorem: ``` local len = math.sqrt(v.x*v.x + v.y*v.y) ``` Because this is so useful, there is a simpler method: ``` local len = v:length() -- or: local len = #v ``` If we divide a vector by it's length, we get a vector whose length is 1. This is a *normalized* vector, also known as the *unit vector*. Again, methods to do this already exist: ``` -- set the length of v to 1: v:normalize() -- return a new vector: the normalized (length==1) copy of v: local direction = v:normalizenew() ``` So now we can calculate a friction force easily: ``` local frictionCoefficient = 0.01 -- (in agent.move) local frictionForce = (-self.velocity):normalize():mul(frictionCoefficient) self.force:add(frictionForce) ``` Of course we could also create a function to vary the amount of friction over space. ### Drag A drag force is similar to friction, but varies proportinally to the square of the object speed, and to the surface area in the direction of movement. (For a circle the surface area is equal in any direction.) ``` local dragCoefficient = 1 -- (in agent.move) local len = #self.velocity local dragForce = (-self.velocity):normalize():mul(dragCoefficient * len * len) self.force:add(dragForce) ``` ### Gravitational attraction Gravitational attraction applies in the direction from object A to object B. The magnitude is the product of the two masses multiplied by a constant factor, and divided by the relative distance squared. ``` local gravitationCoefficient = 1 -- (in agent.move) -- get the relative vector from self to the source of gravity: local relative = source.location - self.location -- get the length: local distance = #relative -- get the direction as a unit vector: local direction = relative:normalize() -- now calculate the force: local gravitationForce = direction * gravitationCoefficient * self.mass * source.mass / (distance * distance) ``` Special care needs to be taken here: if the distance between objects is very low, then the force can become astronomical. It makes sense therefore to limit the distance to a safe minimum: ``` local distance = math.max(0.01, #relative) ``` If you want to simulate gravitational attraction between all agents, you could put this into a loop over all the agents. Be careful to not apply gravitation to the object itself! ``` for i = 1, #agents do local source = agents[i] if source ~= self then -- insert gravitational forces end end ``` ### Springs The direction of a spring force is the same as the relative vector between the ends. The magnitude of a force of a spring is proportional to the deviation from it's resting length. So if a spring's natural length is 0.1, but the current length is actually 0.4, then the spring force is proportional to -0.3. The spring force also includes a scaling coefficient. Spring forces can quickly lead to oscillation. A damping filter is usually required to allow oscillation to fade away. ### Rotational forces If a force applied to a body is not applied at the center of mass, it will add a rotational force, setting the body into rotation. Everything we have said for location can also be said for rotation. The orientation of an object, which in 2D space is just an angle relative to the coordinate system (which you could thus use in draw2D.rotate() for example); it is the angular equivalent of location. The angular equivalent of velocity is angular velocity, which is also a single angle in 2D. And so on for acceleration and forces (torque). Since in 2D angles are scalar values, integration is simply addition. Similarly, there can be rotational friction, rotational springs, and so on. ## Intentional forces So far we have concentrated on physical forces external to an agent, but we can also consider the agent's ability to apply forces to itself (locomotion). Different situations call for different strategies, and these lead to different forces being applied. Hunting, chasing, evading, random walk exploration, chemotaxis, avoidance, copying, centering, swarming... This is discussed in a previous course [here](http://grrrwaaa.github.io/gct753/agent.html), and in particular Craig Reynold's excellent paper [Steering Behaviors for Autonomous Characters](http://www.red3d.com/cwr/steer/gdc99/).