Evolutionary Systems

There have been more than four decades of computational systems inspired by natural evolution. It has become a major field of machine learning and optimization. Beyond AI, it has been used in hardware and circuit design, robotics, and more recently in industrial design and architecture. It has of course also been deeply explored in art and music.

Karl Sims

Natural evolution

The theory of natural evolution combines population, diversity, heredity and selection. Evolution requires a population of individuals that exhibit diversity (both similarities and variations between each other, both within and between species). These individuals can produce new individuals; offspring that exhibit similarites with the parent(s) through heredity. However not all of the population can successfully reproduce. Any factor that affects the possibility of an individual reproducing, thus also affects what characteristics are inherited in the population as a whole. Charles Darwin's theory of natural selection, proposed in 1859, is that the section of the population that can reproduce is not entirely random, but rather is regulated by interactions between inherited characteristics and environmental constraints (such as available food, populations of symbionts, predators and parasites, and so on). Accordingly, the characteristics of a species may change over time (evolution), forming a history that can be investigated through the fossil records.

Origin of the Species

Genetics and the modern synthesis

In 1865 Mendel proposed that characteristics are transmitted to offspring through particles of matter (which we now call genetic material). Schroedinger conjectured that these materials must be aperiodic crystals, and the actual structure of DNA was identified several years later. The "modern synthesis" in biology today has integrated genetics with natural evolution, through the interaction of genotypes and phenotypes:

Hence the modern synthesis requires not only a model for how variation is introduced, but also how genetic material is transfered and how the phenotype emerges from the genotype (development), and what other roles it plays. It is increasingly being understood how the complexity of the environment and materials of life are likely as much or more responsible for the variety of life than the genes themselves.

Briefly: a biological cell contains a vast array of different proteins, whose concentrations determine structures and behaviors of the cell. The proteins are specifed by information in the DNA genetic material (grouped physically into chromosomes). When a cell reproduces by mitosis, a copy of the DNA is made in the new cell. The sections of a DNA chromosome that code for behavior are called genes. These regions are constantly being transcribed, producing a specific RNA strand for each coding gene region which is in turn used to produce a specific protein; the protein string immediately folds up (in a way we cannot yet simulate) into a particular reactive shape which specifies the protein's behavioral role in the cell. This is a one-directional flow of information: Coding DNA -> RNA -> folding -> active protein. In addition to coding regions genes may also have regulatory region which can react with specific proteins to activate or inhibit the coding-protein system, forming a complex regulatory network of interactions by which one gene can activate or inhibit another, and also specify changes of behavior of a cell according to environmental conditions such as chemical signals. These networks can be fantastically complex even in very simple organisms, according to the scientific results of functional genomics. Between the coding and regulatory regions of DNA, there are huge sections of nongenic DNA, whose role (or lack thereof) is not yet understood.

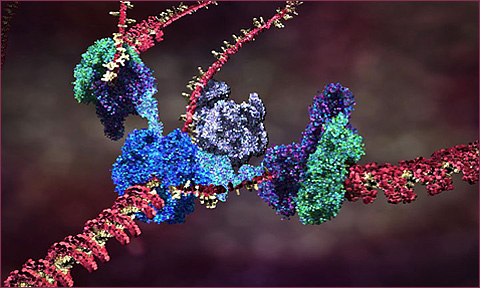
Rendering

The current theory of cell replication and DNA transcription been beautifully illustrated by Drew Berry; and more of his animations here

Genetic variation can occur during replication of the genome, such as copying-error mutations (reversals of segments, insertion & removal of segments, changing individual elements in the sequence, and pair-wise substitution over whole sections) and recombination (taking sections from two different parent genes to construct a new child gene).

Artificial evolution

Artificial evolution is a form of computational simulation whose process mirrors the abstract structure of natural evolution. Broadly it comprises:

The system is then run by these steps:

  1. Initialization of a 'seed' population of genotypes
  2. Development of phenotypes from the genotypes
  3. Evaluation and selection of best/viable candidates of phenotypes, according to fitness criteria or ongong viability conditions, to choose who may reproduce.
  4. Reproduction, creating new genotypes by applying mechanisms of variation, according to variation rates/probabilities.
  5. Repeat from step (2) or terminate if a terminating condition is satisfied (such as sufficient fitness).

Steps 2-5 may be run in lock-step, or asynchronously with overlapping individual life-spans.

The main systematic differences between this an natural evolution are that the underlying mechanisms specified by us in advance, as are the initial populations and the method of selection and/or environmental conditions. And of course, artificial evolution occurs in a much simpler substrate than real chemistry.

A fantastic list of practical applications of genetic algorithm & evolutionary programming

Some inspiration

Karl Sims' Genetic Images -- and the 1991 Siggraph Paper

Karl Sims: Evolving 3D Morphology and Behavior by Competition, 1994:

Scott Draves, “Evolution and Collective Intelligence of the Electric Sheep,” The Art of Artificial Evolution, 2008.

High Fidelity Sample from Scott Draves on Vimeo.

Evolving 2D cars Evolving soft robots Evolving neural networks to play Mario:

An excellent discussion of the genetic algorithm in art and its relation to Deleuze, by Manuel Delanda

A trivial string generator

Just to practice the mechanics, we can start by evolving sentences toward a desired result. Each gene is an integer, which is mapped to a word from a predefined list:

// the desired result:
let target = "the quick brown fox jumped over the lazy dog";

// the set of components:
let dictionary = ["I", "a", "an", "bleep", "blown", "bog", "box", "broad", "brown", "bumped", 
    "cat", "cog", "coloured", "colourful", "colourless", "crazy", "creep", "crown", "dig", 
    "do", "dog", "door", "dot", "ever", "fit", "fix", "flick", "for", "fox", "frown", 
    "glean", "great", "greed", "green", "greet", "hazy", "he", "hog", "ideas", "idols", 
    "in", "it", "jumble", "jumped", "jumper", "jumps", "last", "lazy", "leaped", "lumped", 
    "maze", "of", "offer", "ogre", "older", "on", "or", "over", "quick", "quite", "rapid", 
    "she", "sheen", "sheep", "sick", "sleep", "slept", "slow", "spelt", "spilt", "the", 
    "town", "under"];

// initial:
let geno = [];
for (let i=0; i < 9; i++) {
    geno[i] = random(dictionary.length);
}
// develop:
let pheno = [];
for (let i=0; i < geno.length; i++) {
    pheno[i] = dictionary[ geno[i] ];
}
pheno = pheno.join(" ");

To evaluate, we could compare how many of the right characters are in the right places:

let err = 0;
for (let i=0; i < pheno.length; i++) {
    if (pheno.substr(i, 1) != target.substr(i, 1)) {
        err++;
    }
}
// make it fair between long & short strings:
err /= pheno.length;

To convert this error into a fitness, where fittest is 1 and least fit is zero, we could apply a 1/(1+n) mapping:

let fitness = 1 / (1 + err);

This gives us all the basic components we need to generate a random population as genotypes. We already know how to develop and evaluate such a genotype, and storing several in a population is trivial.

It is generally useful to sort a population by fitness, which can be done like so:

// sort the population by comparing pairs
// as a result, the fittest candidate will be in population[0]
population.sort(function(a, b) { return b.fitness - a.fitness; });

After sorting it is convenient to print out the candidates, their fitness, etc, so we can see how the evolution proceeds.

After evaluating, we create a new generation of candidates, broadly derived from the previous, but with fitter candidates being more likely to be progenitors. The simplest method is to pick a parent at random, but biasing toward the lower indices. (A simple trick to do this is for the nth child to use a the parent at index random(n).)

This is called stochastic universal sampling: it draws samples from the entire range, but selects fitter individuals more often than less-fit candidates.

We must also introduce some variation (mutations) while generating new genotypes at this point. The simplest method is to introduce a branch with a predetermined probability to randomize a gene rather than copy from the parent, e.g.:

// copy or mutate genes:
for (let j = 0; j < gene_size; j++) {
    // mutate?
    if (random() < mutability) {
        child[j] = random(gene_range); 
    } else {
        // copy:
        child[j] = parent[j];
    }
}

Does it work? If not, can you think of ideas why -- and any ideas to improve it?

Does it sometimes seem to get stuck? Can you suggest why? Can you think of any way to modify the mutation, evaluation, or even the genetic representation to overcome this?

As a variant, we could evaluate success based on the concept of the longest common substring:

// an algorithm to return the longest common substring of two strings
// transcribed from https://en.wikipedia.org/wiki/Longest_common_substring_problem
function longest_common_substring(s, t) {
  let L = new Array(s.length);
  let z = 0; // length of the longest common fragment so far
  let ret = "";
  for (let i = 0; i < s.length; i++) {
    L[i] = new Array(t.length);
    for (let j = 0; j < t.length; j++) {
      if (s[i] == t[j]) {
        let v = 1;
        if (i > 0 && j > 0) {
          v = L[i - 1][j - 1] + 1;
        }
        L[i][j] = v;
        // is this the longest we found yet?
        if (v > z) {
          ret = s.substring(i - v + 1, i + 1);
          z = v;
        }
      } else {
        L[i][j] = 0;
      }
    }
  }
  return ret;
}

As an extension, can you imagine working from a much larger lexicon of words, and coming up with a fitness measure that evaluates according to how much sense a randomized sentence makes? Perhaps take a look at n-grams, and/or grammar parsing, and/or methods used in natural language generation.

Or, since English syntax and semantics are pretty hard, how about generating random but syntactically correct programs?

A simple math solver

The string example was a little silly, but let's say we want to write a program (the phenotype) that can solve math problems. To start as simple as possible, we can restrict our programs to numerals and symbols of basic arithmetic:

let symbols = ["+", "-", "*", "/", "1", "2", "3", "4", "5", "6", "7", "8", "9", "0"];

To generate a random program, of say, length 10 characters, and run it, we would do something like this:

// fill an array:
let arr = [];
for (let i=0; i<10; i++) {
    // pick a symbol at random to add:
    arr[i] = symbols[random(symbols.length)];
}
// convert the array of symbols to a string of code:
let code = "return " + arr.join("");
// convert to an executable function:
let f = new Function(code);
// run it to get the result
console.log(f());

The chances are, the generated code is garbage, and might well throw an error, or return a meaningless result such as Infinity or NaN. These errors could break or throw off our simulation, but we can trap them safely as follows:

try {
    // convert to an executable function:
    let f = new Function(code);
    // run it to get the result
    let result = f();
    if (result != Infinity && result != -Infinity && result == result) {
        console.log(result);
    }
}

Now we can evaluate the fitness of our result, relative to a target number. We can take the absolute difference, and then put this through a 1/(1+n) mapping as before. This mapping is somewhat arbitrary, but works for our purposes here:

fitness = 1 / 1 + (Math.abs(result - target));

With this in play, we should already see some clear evolutionary behaviour. You may notice punctuated equilibria. Run the simulation many times, and you may notice that the fittest candidate is not always converging to the same result. There are clearly multiple distant fitness peaks here.

You may notice that the code generated sometimes looks odd -- and that the evolution has discovered tricks such as adding numbers multiplied by zero, prefixing zeroes to numbers, and even placing two slashes to create a comment (followed by "junk DNA"), in order to get a result with the specific gene length. We could easily prevent this by turning our "/" symbol into a " / " symbol, but perhaps there is an advantage not to?

Try changing the genome size, the population size, and the mutation rates, to see how it changes.

Try playing with the symbol list. What happens if you add the "." character? How about "(" and ")"?

The mutation rate acts a bit like a temperature control -- too high and good results can't remain viable, too low and it takes to long to get anywhere. Larger populations help to generate more chances of leaping off a local peak. Too short genome sizes can be a tough challenge, but too long genomes make it less likely to find a result quickly -- and add more noise. Is there a way to make genome size variable, and give shorter results higher fitness? What other mutation methods could help? What other developmental models could be tried? Is there a better way to pick parents?

Generally, by observing the behaviour, what insights can you draw, and what ideas have you for improving it?

How would you be able to add operators such as Math.sin()?

What other problems could you imagine addressing, other than calculating numbers? (What kinds of problems is this method suited for?)

Tournament Selection

We can continue using the fitness-proportionate selection as before, via stochastic universal sampling, however many systems use a different form of selection known as tournament selection, in which a number of individuals are chosen at random from the population to create a temporary neighbourhood set, and the fittest of this neighbourhood set is chosen as parent to create a new individual. (Or sometimes, a weighted probability veering toward the fittest in the neighbourhood set, to make it less deterministic.)

In part this helps to mirror the spatial/network effects of populations, in that it is unlikely for every member of a population to meet every other; selection is made on the somewhat random subset of the population that is encountered.

Selection pressure is easily adjusted by changing the tournament neighbourhood set size. If the size is larger, weak individuals have a smaller chance to be selected.

Genetic representation

Many systems represent genetic information as a sequence of data, such as a string of characters or binary digits. Some systems use more elaborate structures (trees, networks), but these are usually reducible to and encoded as linear sequences. After all, our genes wind up in complex structures with different reactive regions, but at the lowest level are just a long singular chain of A, G, C or T molecules.

The simplest systems have a fixed length, but nature shows quite a lot of variance (not particularly correlated with the size, complexity, or evolutionary age of a species).

Initializing the genotypes implies generating randomized candidates that stay within its bounds but hopefully give a sufficiently diverse range of the possibilities of the genotype. For a simple sequence of bits, symbols, or numbers, this is fairly easy to do.

Development

In some systems the developmental process is little more than a trivial mapping, but this potentially misses an entire and fascinating source of diversity. Incorporating more complex developmental models can lead to geometric variations that are not stored as simple parameters, to repeated segments and recursive structures, to symmetries, and to the re-application of common toolboxes toward a widely differing set of purposes -- all things that are evident in biological evolution.

Selection

For problem solving in data mining, engineering, design, architecture, etc.: If the fitness criterion is static and designed around a particular problem we wish to find a solution for, evolution can help evaluate & test candidate solutions and selectively breed them to produce better solutions, ideally converging on an optimal one, without having to understand or derive by proof. It is a form of optimization. However this process may take a long time or a lot of processing power to find a satisfactory result, or may not reach a result at all. Not all problems are suitable for evolutionary search.

Evidently, these systems differ markedly from natural evolution by having a static measure, and thus a singular teleological character, a meaningful sense of progress, across the entire history of the system. This is more akin to selective breeding than natural evolution.

Note that simply taking the best candidate alone is not necessarily the ideal strategy; selecting randomly by proportion to fitness ("roulette wheel" selection) may better overcome local maxima.

For art, music, and other less formalized domains we may need to consider other methods of selection, since a formal measure may not be possible, or the problem may not be clearly statable in advance. E.g. can we measure aesthetic quality in formal terms?

Variation

The mechanisms of variation possible partly depend on the representation chosen. The two most common principles of variation in artificial evolution are naturally inspired:

Why use reproduction for evolution? In the face of an unpredictable environment, we cannot know which strategy will be best; we can try small variations, and hedge our bets by making very many of them (population diversity). An individual loss is not catastrophic, but a few successes can be learned from. Furthermore, the face of unpredictibility implies that what was true today may not be tomorrow, so the flexibility to avoid timeless commitment is also a good strategy; but the inheritance of choices is a useful option when the environment retains some stability. If the world were fully predictable, a rational, teleological, monothematic strategy would be preferable. But the world isn't totally random either (if it was, there would be no valid strategy worth pursuing.)

As with temperature-like parameters we saw in CA, a crucial factor in evolution is the rate or probability of variation. Too much, and the population may never significantly diverge from a randomly initialized one; too little, and it may find itself stuck on the first solution it finds, with a largely homogenous population. It may be wise to have different mutation rates for different genes, or for different members of a population, or by fitness rank etc. It is likely desirable to gradually reduce mutation rates over time, unless the population appears to be stagnating. (See also simulated annealing.)

Aesthetic selection of biomorphs

Biomorphs are virtual entities that were devised by Richard Dawkins in his book The Blind Watchmaker as a way to visualize the power of evolution. Dawkins used a simple symbolic rendering of lines at fixed angles, grown in a kind of tree structure, as his phenotypes. Of a given generation, he selected the biomorph he found most aesthetically pleasing, making this the parent of the next generation.

biomorph

Adding new lines (or removing them) based on simple developmental rules offered a discrete set of possible new shapes (mutations), which were displayed on screen so that the user could choose between them. The chosen mutation would then be the basis for another generation of biomorph mutants to be chosen from, and so on. Thus, the user, by selection, could steer the evolution of biomorphs. This process often produced images which were reminiscent of real organisms for instance beetles, bats, or trees. Dawkins speculated that the unnatural selection role played by the user in this program could be replaced by a more natural agent if, for example, colourful biomorphs could be selected by butterflies or other insects, via a touch sensitive display set up in a garden.

Aside: Turtle graphics

We'd like to generate biomorphs in a similar way. What we want to create is a function that maps genome strings into biomorph shapes. The genotype is a string of symbols, the phenotype is the graphics that result.

The biomorphs are all made out of simple line drawings. For efficiency, we can use the draw2D.lines() method to draw a list of lines at once. Here's how it works:

// draws a plus (two pairs of points for each line)
draw2D.lines([
    [0.2, 0], [0.8, 0], // the horizontal line
    [0, 0.2], [0, 0.8], // the vertical line
]);

The classic example is using the genotype strings as instructions for a "turtle graphics" interpreter. A minimal alphabet & semantics could be something like this:

To draw in the Turtle style, we need to represent a turtle's properties, which are a position and a direction. Then, we can manipulate these properties to capture the turtle's movement, collecting points of a line as it moves.

We can start by building a function that creates a turtle, and uses it to collect points to draw a specific shape, such as a square.

Be careful to insert copies of the turtle location into the list of line points, rather than insert a reference. If we didn't clone a copy of the point, we would end up with many references to the same vec2 object in the list.

It should be apparent that the code is highly repetitive. Conceptually, we could instead represent this as a data structure: a list of commands such as "forward, turn, forward, turn, forward, turn, forward". Let us rewrite our function as an interpreter of such a list of commands. This becomes powerful as it would allow us to generate different shapes in a data-driven way, simply by passing in a list of commands. We could even compress these commands to simple turtle mnemonics, of "F+F+F+F".

Once we have an interpreter, we could go one step further and turn into a compiler; a compiler is just an interpreter that generates executable code rather than executes code. We can take our interpreter and change all of its actions into the generation of strings of code, collecting all these lines of code into a big list. Finally, we join all those strings together (with newlines between) and convert them into a new Function. With this we can generate any arbitrary string of commands and turn it into a re-usable graphics function!

And, of course, since these functions are generated from strings, they can be generated from string genomes!

With this in place, we could now expand our vocabulary of actions in our mini-language, to include things like these:

We could also make our shapes more dynamic. For example, we could generate rotation angles in the function according to the current time (e.g. let a = Math.sin(now)).

One of the advantages of using strings of symbols as genotypes is their readability, but another is the flexibility to perform different kinds of mutations:

Some of these mutations can change the length of the string. It may be advisable to add limits on the minimum or maximum length of the string mutations can produce.

Now we can show all members of a generation side-by-side, and use the mouse to choose the member we prefer to form the parent of the next generation.

Possible extensions:

The past point is important to consider. A convincing form of bilateral symmetry (something found in many organisms) can be achieved by L-system production rules, rather than by embedding this into the interpreter.